Sankt-Peterburg shahridagi mashhur 239-maktabning matematika olimpiadasida berilgan quyidagi geoni (P2, Senior, 2023) qaraylik:
▻ Aytaylik, bizga $ABC$ uchburchak berilgan va uning tashqi-ichki aylanalari $BC$, $CA$, $AB$ tomonlariga mos ravishda $A_1$, $B_1$, $C_1$ nuqtalarda urinadi. $BB_1$ va $CC_1$ kesmalarning o`rtalari mos ravishda $B_2$ va $C_2$ bo`lsin. Aytaylik, $B_2C_2$ va $BC$ to`g`ri chiziqlar $W$ nuqtada kesishadi. U holda $WA=WA_1$ ni isbotlang.
Masalada biz bilgan konfiguratsiya yashiringan. Uchburchak tomonlarida $B_1$ va $C_1$ nuqtalar olingan bo'lib, $BC_1=CB_1$ shart bajariladi deb qarashimiz mumkin.
-------------------------------------------------------------------
Yechish. Ma'lum-ki, $BC_1=CB_1=p-a$ va oldin ko'rgan masalamizga ko'ra, $\overline{B_2C_2}\perp \overline{u}$, bu yerda $\overline{u}$ - $\angle A$ ning bissektrisasi yo'nalishidagi birlik vektor.
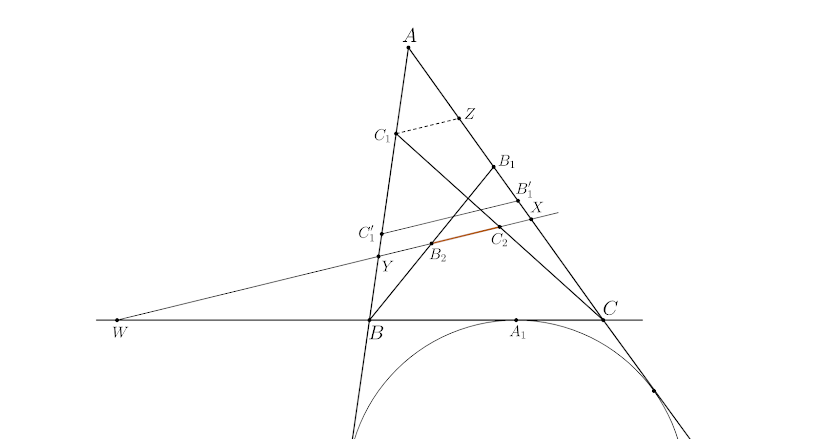 |
| 1-chizma |
Aytaylik, $B_2C_2$ to'g'ri chiziq $AB$ va $AC$ tomonlarni mos ravishda $Y$ va $X$ nuqtalarda kesadi. U holda $AY=AX$ bo'lar ekan. Faraz qilaylik, $Z$ nuqta $AC$ tomonda olingan va $C_1Z\| B_2C_2$ bo'lsin (1-chizma ga qarang). Biz bilamiz-ki, $AC_1=AZ=p-b$ va $CZ=2b-p$. Unda \[ AX=AZ+ZX = p-b +\frac{2b-p}{2} = \frac{p}{2} \] bo'ladi, va bundan \[ \mathrm{Pow}_X (A(.)) = \mathrm{Pow}_X (\omega_a) \] keladi, bu yerda $A(.)$ sifatida $A$ markazli nol-radiusli aylana, $\omega_a$ sifatida esa uchburchakning $A-$tashqi-ichki aylanasi nazarda tutilmoqda. Xullas, $X$ nuqta $A(.)$ va $\omega_a$ aylanalarning radikal o'qida yotadi. Xuddi shunday, $Y$ nuqta ham ushbu aylanalarning radikal o'qida yotishini ko'rsata olamiz. Demak, $W$ ham ushbu radikal o'qda, va bundan $WA=WA_1$ bo'lishi ayon. Isbot tugadi. ▢