IMO2017/P4:
▻ $\Omega$ aylana va unda yotadigan $R$, $S$ nuqtalar berilgan, bunda $RS$ aylana diametri emas. Ushbu aylanaga $R$ nuqtadan $\ell$ urinma o'tkazilgan. Aytaylik, $RS$ to'g'ri chiziqda $T$ nuqta shunday tanlangan-ki, bunda $S$ nuqta $RT$ kesmaning o'rtasi bo'ladi. Bundan tashqari, $\Omega$ aylananing $RS$ kichik yoyida $J$ nuqta shunday tanlangan, bunda $JST$ uchburchak tashqi aylanasi bo'lmish $\Gamma$ aylana $\ell$ to'g'ri chiziqni ikkita turli nuqtalarda kesib o'tadi; $A$ ushbu nuqtalarning $R$ ga yaqinrog'i bo'lsin. Aytaylik, $AJ$ to'g'ri chiziq $\Omega$ aylanani ikkinchi bor $K$ nuqtada kesadi. U holda $KT$ to'g'ri chiziq $\Gamma$ aylanaga urinma bo'lishini isbotlang.
Yechim. Albatta, $AT$ va $SJ$ lar o'zaro antiparallel bo'lsa, $RK$ bilan $SJ$ lar ham o'zaro antiparalleldir. Xullas, $\angle TAJ = \angle JSR = \angle JKR$ va $AT\parallel RK$ kelib chiqadi. Ushbu parallellikdan $\angle ATR = \angle SRK$ ekanligi bizda bor. Boshqa tomondan, $\ell$ ning $\Omega$ ga urinma ekanligidan $\angle ART = \angle SKR$ ni ham topishimiz mumkin. Demak, $\triangle ATR \sim \triangle SRK$.
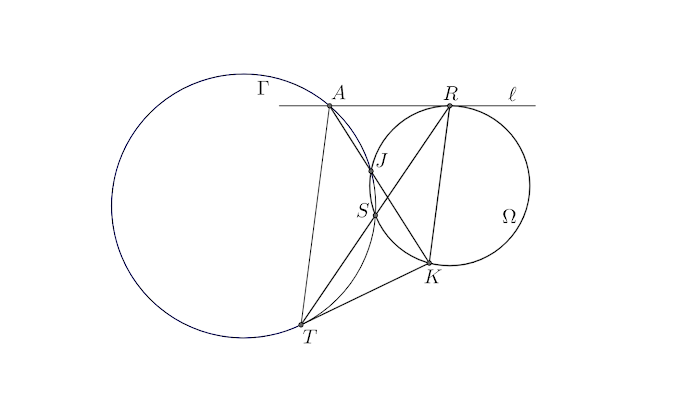 |
| 1-chizma |
Ushbu o'xshashlikdan $\frac{AT}{TR} = \frac{SR}{RK}$ ni yoza olamiz. $S$ nuqtaning $TR$ kesma o'rtasi ekanligidan esa $\frac{AT}{TS} = \frac{TR}{RK}$ ekanligi ham keladi. Demak, $\triangle ATS \sim TRK$, chunki $\angle ATS = \angle TRK$ edi. Aynan ushbu o'xshashlik, bizga $\angle TAS = \angle RTK$ ni beradi, ya'ni $KT$ to'g'ri chiziq $\Gamma$ aylanaga $T$ nuqtada urinadi. ▢